Question

The equation below represents Function A and the graph represents Function B:

Function A

f(x) = x − 9

Function B (image)

Which equation best compares the slopes of the two functions?

a) Slope of Function B = 2 x Slope of Function A.
b) Slope of Function A = Slope of Function B
c) Slope of Function A = 2 x Slope of Function B
d)Slope of Function B = − Slope of Function A

Answer 1

We have the equation for function A. Is is a line, already written in the form
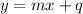`y = mx+q`. In these cases, the slope of the line is
`m`. So, the slope of function A is 1.

As for function B, we have to pick two of its graph's point, say
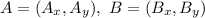`A = (A_x,A_y),\ B = (B_x, B_y)` and compute the slope as follows:

`m = \cfrac{\Delta y}{\Delta x} = \cfrac{A_y-B_y}{A_x-B_x}`

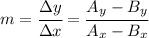
We can see that the function passes through the points
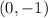`(0,-1)` and [/tex] (1,1) [/tex]. So, its slope is

`\cfrac{-1-1}{0-1} = \cfrac{-2}{-1} = 2`

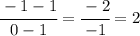
So, the slope of function A is 1, and the slope of function B is 2.

This means that the first option is correct.