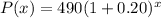Question

What equation represents a population of 490 animals that increases at an annual rate of 20%

Answer 1

The equation i.e. used to denote the population after x years is:

`P(x)=490(1+0.20)^x`

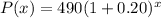
Explanation:

This problem could be modeled with the help of a exponential function.

The exponential function is given by:

`P(x)=ab^x`

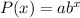
where a is the initial value.

and b=1+r where r is the rate of increase or decrease.

Here the initial population of the animals are given by: 490

i.e. a=490

Also, the rate of increase is: 20%

i.e. r=20%

i.e. r=0.20

Hence, the population function i.e. the population of the animals after x years is:

`P(x)=490(1+0.20)^x`