Question

Isabella filled her pool with water at a constant rate.

The table compares the remaining volume of water left to fill the pool (in liters) and the time since Isabella started filling the pool (in minutes)
How fast did Isabella fill her pool?

Answer 1

The rate at which Isabella filled her pool is −18 liters per minute.

To determine how fast Isabella filled her pool, we can calculate the rate of water filling by finding the slope of the line that represents the relationship between time and water volume.

The slope of the line is the rate of change of water volume with respect to time.

Let's use the points (2, 184) and (12, 4) from the table.

The formula for calculating the slope (rate) is:

Rate=
`(Change in water volume)/(Change in time)`

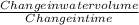
​Substitute the values:

Rate=
`(4-184)/(12-2)`

Rate=
`(-180)/(10)`

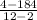
Rate=−18

So, the rate at which Isabella filled her pool is −18 liters per minute. The negative sign indicates that the water volume is decreasing over time, which is expected as the pool is being filled.

Answer 2

General Idea:

When we are given Time ' t ' in minutes and Volume ' V ' in liters, the speed at which the volume changes is given by its slope. That is change in Volume with respect to Change in time.

`m = (V_(2)-V_(1))/(t_(2)-t_(1))`

Applying the Concept:

From the table picking the first two points (2, 184) and (7, 94)

`image`

Conclusion:

The rate at which Isabella fill her pool = 18 liters/minute