Question

The equation models the height "h" in centimeters after "t" seconds of a weight attached to the end of a spring that has been stretched and then released.

h= 7cos(pi/3 t)

a. Solve the equation for t
b. Find the times at which the weight is first at a height of 1 cm, of 3 cm, and of 5 cm above the rest position. Round your answers to the nearest hundredth.
c. Find the times at which the weight is at a height of 1 cm, of 3 cm, and of 5 cm below the rest position for the second time. Round your answers to the nearest hundredth.

Please explain each step! Thank you!!!

Answer 1

a. Solve for t the way you do any "solve for" problem: undo the operations that are done to the variable of interest. The inverse operation for the cosine function is the arccosine function.

`h=7\cos{\left((\pi)/(3)t\right)}\\\\ (h)/(7)=\cos{\left((\pi)/(3)t\right)}\\\\ \arccos{\left((h)/(7)\right)}=(\pi)/(3)t\\\\ t=(3)/(\pi)\arccos{\left((h)/(7)\right)}`

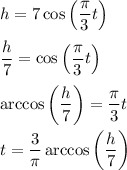
b.

For h=1 cm, t ≈ (3/π)arccos(1/7) ≈ 1.36 seconds

For h=3 cm, t ≈ (3/π)arccos(3/7) ≈ 1.08 seconds

For h=5 cm, t≈ (3/π)arccos(5/7) ≈ 0.74 seconds

c. The period of the oscillation can be found by setting (π/3)t = 2π and solving for t. That value is t=6. Due to the symmetry of the cosine function, the times of interest for this part will be 1 1/2 periods less the times found in part b.

For h=-1 cm, t = (1.5×6) - 1.36 = 7.64 seconds

For h=-3 cm, t = 9 - 1.08 = 7.92 seconds

For h=-5 cm, t = 9 - 0.74 = 8.26 seconds

_____

Note that when you use your calculator to find the arccos( ) values, it must be in radians mode, not degrees mode.