In an arithmetic sequence d represent the common difference.
The formula to find the general term of an arithmetic sequence is,
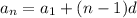
Where
 = nth term and
= nth term and
 = First term.
= First term.
Given,
 . Therefore,
. Therefore,
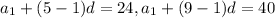

Next step is to subtract the above equations so that we can eliminate a1 and get the value of d. Hence,
4d - 8d = 24 - 40
-4d = - 16
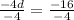 Divide each sides by - 16.
Divide each sides by - 16.
d = 4
So, d = 4.
Hope this helps yoi!.