Question

A two digit number when read from left to right to right consiststs of consecutive integers. the nmber is six more than for times the sum of its digits

Answer 1

I suppose you want to know such number. Since we have a two digit number consisting of two consecutive integers, the only possible numbers are:

`12,23,34,45,56,67,78,89`

Since we sorted all the cases out, we simply have to check which one satisfies the requirement. For each number, we'll write four times the the sum of its digits, and add 6, hoping to get the original number.

`\text{Number: } 12,\ \ 4* \text{sum of digits: } 12\ \ \text{plus six: } 18\\eq 12`

`\text{Number: } 23,\ \ 4* \text{sum of digits: } 24\ \ \text{plus six: } 30\\eq 23`

`\text{Number: } 34,\ \ 4* \text{sum of digits: } 28\ \ \text{plus six: } 34`

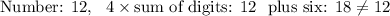
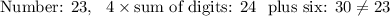
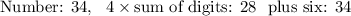
So, the answer is 34.