Question

Find the area of the triangle whose vertices are (0,4) , (0,0) and (2,0) by plotting them on graph

Answer 1

Refer to the attached image. Since one vertex is the origin and the other two lay on the coordinate axes, the triangle is a right triangle. This means that, if we consider AB to the be base, AC is his height, and vice versa.

Anyway, it means that the area is given by

`A = \cfrac{\overline{AB}*\overline{AC}}{2}`

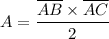
Since AB is a horizontal segment and AC is a vertical segment, their length is given by the absolute difference of the non-constant coordinate: points A and B share the same x coordinate, so we subtract the y coordinates:

`\overline{AB} = |2-0| = |2| = 2`

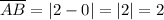
The opposite goes for AC: points A and C share the same y coordinate, so we subtract the x coordinates:

`\overline{AC} = |4-0| = |4| = 4`

So, the area is

`A = \cfrac{2* 4}{2} = 4`