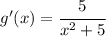Question

Let g(x) be defined by: g(x)=int_1^x 5/(t^2+5)text( )dt determine g'(x). no work needs to be shown.

Answer 1

The integral and the derivative are two opposite operators. It's the same thing as saying that doubling a number and halving it are the opposite, or that squaring a number and taking its square root are opposite operators.

In all cases, if the first operator takes you one step further, the other takes you one step back, returning to the original input.

So, if you define a function by integral, it means that you start from
`f(x)` and define
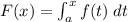`F(x) = \int_a^x f(t)\; dt`. So, when you derive
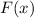`F(x)`, you're going back to
`f(x)`, following this path:

`\text{start: } f(x) \xrightarrow{\text{integrate}} F(x) \xrightarrow{\text{differentiate}} f(x)`

So, you have

`g'(x) = \cfrac{5}{x^2+5}`