we are given equation of line
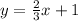
Equation of perpendicular line:
Firstly , we will find slope of line
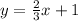
we can compare it with
y=mx+b
we get
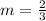
we know that
slope of perpendicular line will be -1/m
so, slope is
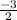
It passes through point (-4,5)
so, we can use point slope form of line
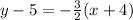
we get
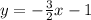 ..........Answer
..........Answer
Equation of parallel line:
Firstly , we will find slope of line
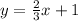
we can compare it with
y=mx+b
we get
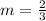
we know that
slope of parallel line always equal
so, slope is
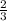
It passes through point (-4,-5)
so, we can use point slope form of line
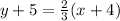
we get
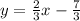 ............Answer
............Answer