Question

Graph the function 
`f(x)= √(x+1)`

Answer 1

Hi there!

Let's solve this problem step by step!

1. To plot the function we must first realise that the function only exists when the root in the function is positive or equal to zero.

Mathematically:

`x + 1 \geqslant 0`

Subtract 1.

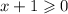
`x \geqslant - 1`

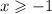
In other words: the function only exists when we plug in values of x that are bigger than or equal to -1.

2. When we plug in x = -1, we find the following:


`f( - 1) = √( - 1 + 1) = √(0) = 0`

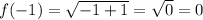
Therefore, the beginning point of the graph is (-1, 0).

3. To find the other points that are located on the graph, we need to plug in different values of x, to find our values of y (remember x bigger or equal to -1). When we have both values we can graph the function.

Examples:

`f(3) = √(3 + 1) = √(4) = 2 \\ f(8) = √(8 + 1) = √(9) = 3`

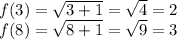
We can also plug in other values of x, but some will make you end up with decimals, which makes the graphing more difficult.

4. The graphed function is attached!
~ Hope this helps you!

Answer 2

howdy!

the points are

1,0 2,1 5,2 !

the second answer is 2,1

goodlucckkk!!!!! <33