Question

The graph represents the function f(x) = 10(2)^x.

Answer 1

General Idea:

The exponential function will be of the form
`y=a(b)^x`.

When b>1, the function indicates the exponential growth.

When 0<b<1, the function indicates the exponential decay.

Applying the concept:

We are given the graph of
`y=10(2)^x`, here b = 2.

The question ask the characteristic of the function when b is in the interval
`1<b< 2`. The attached figure shows few graphs of exponential function whose b value is less than 2 and greater than 1. We can notice that graph increases at slower rate, that is change in y with respect to change in x is getting slower as we reduce the values of b less than 2 and greater than 1.

Conclusion:

"The graph will increase at a slower rate"

Answer 2

Answer: Hence, Third and Fourth options are correct.

Explanation:

Since we have given that

`f(x)=10(2)^x`

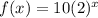
Since it is in the form of exponential function:

As we know the general form of exponential function is given by

`f(x)=ab^x`

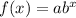
Here, a denotes the initial amount.

b denotes the rate of growth.

If b is decreased but remains greater than 1.

Then, the graph will still increases but in slower rate.

and the value of y continue to increase as x increases.

Hence, Third and Fourth options are correct.