Question

99 POINTS!!! JUST ANSWER THIS QUESTION, PLEASE!!!

a parallelogram has vertices at (1,3),(5,-9),(8,3),and (-2,-9). Where do the parallelogram's diagonal intersect?

Answer 1

Hi!

I would approach this question by first looking at where the parallelogram is located, by graphing the image. I did so and drew a rough image on Paint (See attached image)

To get the part where the diagonals intersect, I would find the midpoint of the line between points (1, 3) and (5,-9) (or the other pair). The reason is a parallelogram's diagonals always bisect each other, meaning the point they intersect is always the middle of the two diagonals.

Therefore, you can find the midpoint of a diagonal, between (1, 3) and (5, -9). The midpoint theorem is (
`(x_(1) + x_(2))/(2), (y_(1) + y_(2))/(2)`.

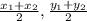Take the points (1, 3) and (5, -9), and fill them in.

`((1 + 5)/(2) , (3 - 9)/(2))`

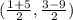
Then solve.

`((6)/(2), (-6)/(2))`

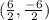
(3, -3)

If you'd like to check the other midpoint:

Take the points, (8, 3) and (-2, -9)

`((8 - 2)/(2), (3 - 9)/(2))`

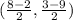
Then solve.

`((6)/(2) , (-6)/(2))`

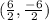
(3, -3)

They're the same, so that answer is correct.

Hope this helps!