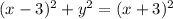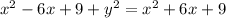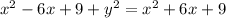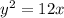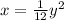Question

Find the standard form of the equation of the parabola with a focus at (3, 0) and a directrix at x = -3.

serious answers only

Answer 1

x = 1/12Y^2 is correct

Answer 2

That's a sideways one; let's go back to first principals.

A parabola is the locus of points equidistant from a point called the focus and a line called the directrix.

It's almost always better to work with squared distance:

The squared distance from (x,y) to (3,0) is
`(x-3)^2 + y^2`

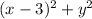
The squared distance from (x,y) to x=-3 is
`(x- - 3)^2`

Equating,

`(x-3)^2 + y^2 = (x+3)^2`

`x^2 - 6x + 9 + y^2 = x^2 + 6x + 9`

`x^2 - 6x + 9 + y^2 = x^2 + 6x + 9`

`y^2 = 12x`

`x = (1)/(12) y^2`