Question

Verify that the hypotheses of the mean-value theorem are satisfied for f⁢(x)=x+1 on the interval [0,63], and find all values of c in that interval that satisfy the conclusion of the theorem. enter the exact answers in increasing order. if there is only one value of c, enter na in the second answer area. note that "c=" is already provided. do not include this in your submitted responses to this question. c=

Answer 1

The mean value theorem states that, given a function
`f(x)` continuous in some interval
`[a,b]` and differentiable in the same open interval
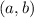`(a,b)`, there exists a point
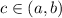`c \in (a,b)` such that

`f'(c) = \cfrac{f(b)-f(a)}{b-a}`

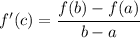
In your case, the function
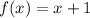`f(x) = x+1` is a polynomial, and as such it is continuous and differentiable infinite times on the whole real number set. So, in particular, it is continuous in
`[a,b] = [0,63]` and differentiable in the same open interval
`(a,b) = (0,63)`.

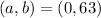Moreover, the derivative of the function is

`f'(x) = 1`

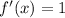
So, the statement of the mean value theorem becomes the following: there exists a point
`c \in (0,63)` such that

`f'(c) = \cfrac{f(63)-f(0)}{63-0}`

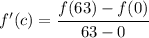
But we know that
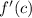`f'(c)` is constantly 1, so we have

`1 = \cfrac{64-1}{63-0} = \cfrac{63}{63}`

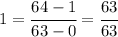
which is an identity, i.e. an equation which is always verified.

So, every point in
`(0,63)` satisfies the mean value theorem.

Why? Well, the theorem states the existance of a point such that the tangent to that point (which is [/tex] f'(c) [/tex]) has the same slope as the secant connecting
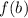`f(b)` and
`f(a)`.

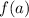But in this case,
`f(x)` is a line, which means that the said secant and the function itself are actually the same thing.