Given exponential function
f(x)=

Where x is the number of years
f(x) is the number of tuna in thousands
To find out when number of tuna is 50 thousand , we plug in 50 for f(x) and solve for x
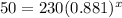
Divide by 230 on both sides
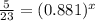
Take ln on both sides
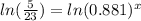
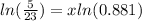
Divide by ln(0.881) on both sides
x =
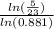
x= 12.04
Year = 1974 + 12.04 = 1986
so in 1986 there will be 50 thousand tuna.