The sum of all measures of interior angles in a polygon with n sides is given by formula
 .
.
The sum of all measures of exterior angles in a polygon with n sides is always
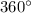 .
.
Then
A) For a pentagon, n=5.
The sum of all measures of interior angles in a pentagon is
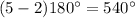 .
.
B) For a 16-sided polygon, n=16.
The sum of all measures of interior angles in a 16-sided polygon is
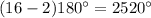 .
.
B) For a dodecagon, n=12.
The sum of all measures of interior angles in a dodecagon is
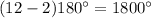 .
.
If these polygons are regular or equiangular, then
A) Interiror angle has measure
 and exterior angle has measure
and exterior angle has measure
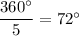 .
.
B) Interiror angle has measure
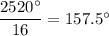 and exterior angle has measure
and exterior angle has measure
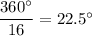 .
.
C) Interiror angle has measure
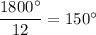 and exterior angle has measure
and exterior angle has measure
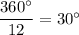 .
.