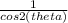Question

Find the polar equation for the cartesian curve x^2-y^2 = sqrt(x^2+y^2)

Answer 1

r =
`(1)/(cos2(theta))`

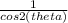
Explaination:

Convert the given curve into the the polar form.

x = rcosθ

y = rsinθ

in f(x,y) = (x²-y²) - √(x²+y²) = 0

put the values of x & y in given curve equation.

We get at,

g(r,θ) = (r²cos²θ - r²sin²θ) - √(r²cos²θ + r²sin²θ) = 0

g(r,θ) = r²(cos²θ - sin²θ) - √r² = 0

We know that,

cos²θ - sin²θ = cos2θ

g(r,θ) = r²(cos2θ) - r = 0

Solve for r

Finally we get:

r =
`(1)/(cos2(theta))`