Trinomials can be factored three different ways: By grouping, With quadratic formula, Completing the square.
Quadratic formula hard to memorize but always works. Its template is:
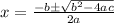
To make quadratic formula work, we need to put the equation into the standard form. In this case, it's already in that form.
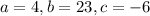
.
When we plug them in:
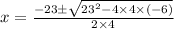
Simplify:
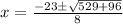
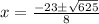

Branch out the plus-minus sign:

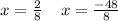
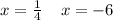
So it's roots are
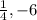
.
Roots of a polynomial are the values which made the equation equal to 0. To make this, we need to write the factored form as

And because
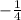
is a fraction, we need to get rid of it. We can do this by multiplying the left side with 4 and our final answer would be
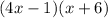
.