Question

Knowing this, you and the company determined that the velocity at which the fireworks should be launched is 224 feet/second. The function that now models the height of the fireworks is f(t) = -16t2 + 224t. A week before the fireworks show, the town manager representative informed you that the fireworks will now be launched from the top of a 120-foot-tall building. Create a new function, g(t), to model the fireworks being shot off the top of the building. Compare the new function with the original function, f(t).

Answer 1

The height of the fireworks from the ground is f(t) =
`-16t^2 + 224t`

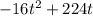
Given that the fireworks will now be launched from the top of a 120-foot-tall building.

In general, the height function h(t) = –16t^2 + v0t + h0

V0- is the initial velocity, h0 is the initial height

Initial velocit = 224

Initial height = 120

So the new function g(t) =
`-16t^2 + 224t + 120`

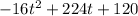
Original function f(t) =
`-16t^2 + 224t`

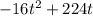
New function g(t)=
`-16t^2 + 224t + 120`

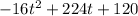
In original function f(x), the firework is launched from the ground so the initial height is 0.

In new function g(x), the firework is launched from the top of a 120-foot-tall building so the initial height is 120.Hence 120 is added with f(x) to get g(x).