Question

Plzzzz help don’t understand

Answer 1

Let v and b represent the numbers of students a van and a bus can carry, respectively. The given information can be expressed as two equations in these two unknowns:

`6v+8b=202\\12v+10b=284`

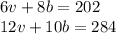
A system of linear equations such as these can be solved many ways. Here, we observe that the coefficient of v in the second equation is double that in the first equation. We can subtract the second equation from twice the first equation and v will be eliminated, leaving an equation in b that we can solve easily.

`2(6v+8b)-(12v+10b=2(202)-(284)\\\\6b=120\qquad\text{collect terms}\\\\b=20\qquad\text{divide by 6}\\\\6v+8\cdot 20=202\qquad\text{substitute for b in the first equation}\\\\v=(202-160)/(6)=(42)/(6)=7\qquad\text{solve for v}`

A van can carry 7 students.

A bus can carry 20 students.