In this question, they gave you the system of equations. You just need to use the two of them.
We want to find the m or the number of the multiple-choice questions. So we need to turn our last equation in the form of 'm's by translating the 'f's into 'm's.
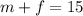
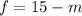
If we know the m form of f, we can convert the second equation and find the answer:

Plug in the m value of f:
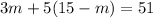
Distribute the 5:
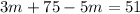
Subtract -75 from both sides:
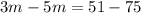
Combine like terms:
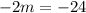
Divide both sides by -2:
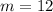
So, we learned that the number of the multiple-choice questions is 12.