15.
We have right triangles, with the ladder the hypotenuse of both and the wall the opposite side of both.
Call the ladder length h.
Against the wall we have the opposite of alpha the taller one:
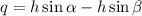
On the ground adjacent to beta is the longer one
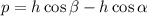
Dividing
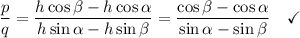
16.
Again I'm too lazy to draw the figure but you should.
Let's call y the height of the tower and x the distance from the observation point on the ground to the base of the tower.
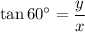
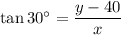
Since
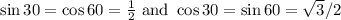
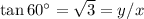
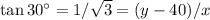
Dividing,
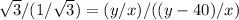
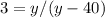
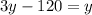
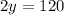
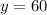
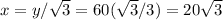
Answer: Height 60 meters, distance 20√3 meters