Question

Help please? I can choose more than one answer I just don’t understand this stuff

Answer 1

`a + 8 = - \frac 5 a`

If I was solving this, which I suppose I am, my first step would be the clear the fractions by multiplying both sides by a.

`a^2 + 8a = - 5`

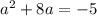
That's there, first choice, SELECT IT

Then I'd bring the 5 to the other side;

`a^2 + 8a + 5 = 0`

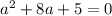
Not among the choices.

Then I'd attempt to factor, looking for a pair that multiplies to 5 and adds to 8; no joy there.

Shakespeare Quadratic Formula (2b or -2b) trick:
`x^2 - 2bx + c \textrm{ has zeros at } x=b\pm √(b^2-c)`

`a = 4 \pm √(4^2-5) = 4\pm √(11)`

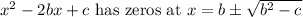
All the other choices have nice rational answers so can't be right.

First choice only