Question

ASAP PLZZZZZZZ

Use properties of limits to find the indicated limit. It may be necessary to rewrite an expression before limit properties can be applied

lim x→1

 
x3 +5 x2 +3x−9 x−1

a. 16
b.-16
c.0

Answer 1

I'm guessing what's really being asked is

`\displaystyle \lim_(x \to 1) (x^3 + 5x^2 + 3x -9)/(x-1)`

Since x=1 is a root of the numerator, we can factor out x-1 which then will cancel with the denominator. Here's the long division; sorry about the lame formatting.

__ x^2 + 6x + 9

x-1 | x^3 + 5x^2 + 3x -9

___ x^3 - x^2

_______ 6x^2 + 3x

_______ 6x^2 - 6x

____________ 9x - 9

____________ 9x - 9

`\quad`

`\displaystyle \lim_(x \to 1) (x^3 + 5x^2 + 3x -9)/(x-1)`

`= \displaystyle \lim_(x \to 1) ((x-1)(x^2 + 6x + 9))/(x-1)`

`= \displaystyle \lim_(x \to 1) x^2 + 6x + 9`

`= 1^2 + 6(1)+9`

`= 16`

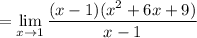
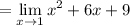
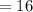
Answer: 16

Choice a