Question

The midpoint of a segment is (−6,−5) and one endpoint is (1,3). Find the coordinates of the other endpoint.

A. (8, 11)
B. (8, -13)
C. (-13, -13)
D. (-13, 11)

Answer 1

C. (-13,-13)
You take the x of the midpoint and equal it to the formula of the midpoint so it will be -6 = 1+x/2 so 1st you times 2 by 6 because you wanna get rid of 2 so it will -12 Then when you move 1 so x is alone it will be -1 so -12-1= -13
Same thing for y

Answer 2

Answer: C. (-13, -13)

Explanation:

The midpoint (x,y) of a line segment having two end points (a,b) and (c,d) is given by :-

`x=(a+c)/(2)\ ;\ y=(b+d)/(2)`

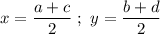
Given : The midpoint of a segment is (-6,-5) and one endpoint is (1,3).

Let the coordinates of other end point be (a,b) then , we have

`-6=(a+1)/(2)\ ;\ -5=(b+3)/(2)\\\\\Rightarrow\ a+1=2*-6\ ;\ b+3=2*-5\\\\\Rightharrow\  a+1=-12\ ;\ b+3=-10\\\\\Rightarrow\ a=-12-1\ ;\ b=-10-3\\\\\Rightarrow\ a=-13,\ ;\ b=-13`

Hence, the coordinates of the other endpoint = (-13,-13)