Question

The area of a rectangle is 70 m ^2

, and the length of the rectangle is 11m less than three times the width. Find the dimensions of the rectangle.

Length: __ m
Width: __ m

Answer 1

A = L * W

Given: The area of a rectangle is 70 m^2

L * W = 70

L = 3W - 11

Substitute L = 3W - 11 into L * W = 70

(3W - 11) * W = 70

3W^2 - 11W = 70

3W - 11W - 70 = 0

(3W + 10) (W - 7)= 0

3W + 10 = 0; W = -10/3 (Dimension can't be negative)

W - 7 = 0; W = 7

L = 3W - 11 = 3(7) - 11 = 21 - 11 = 10

Answer

Length: 10 m

Width: 7 m

Answer 2

Given that the area of rectangle = 70 square meter

We know the formula of rectangle = l * b

where "l" represent the length of the rectangle

and "b" represent the width of the rectangle.

Suppose that width of the rectangle = x

length of the rectangle = 3x - 11

Area = x(3x-11)

70 = x(3x-11)

70 = 3
`x^(2)` - 11x

Now solve the quadratic equation:

We get x = -
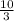`(10)/(3)` and x=7

We negelct the negative value because side length never be negative.

So, width = 7 meter

length = 3x-11

put x=7

length = 3*7 - 11

= 21 - 11

l = 10 meter