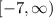Question

Use the function f(x)=3x^2-12x+5

locate the axis of symmetry--
list domain--
list range--

Answer 1

we are given function as

`f(x)=3x^2-12x+5`

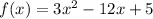
Axis of symmetry:

we can use formula to find axis of symmetry

`f(x)=ax^2+bx+c`

`x=-(b)/(2a)`

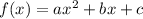
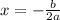
a=3 , b=-12

`x=-(-12)/(2*3)`

now, we can solve for x

`x=2`

so, axis of symmetry is
`x=2`.........Answer

Domain:

we know that

domain is all possible values of x for which any function is defined

since, it is quadratic function

so, it is defined for all real values of x

so, we get

`(-\infty,\infty)`

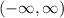
Range:

we know that

range is all possible value of y

we can plug vertex x=2 into f(x) and find y

`f(2)=3(2)^2-12(2)+5`

`y=-7`

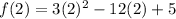
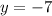
Since, we have leading coefficient is 3

so, parabola will be open upward

so, smallest y-value will be -7

so, range will be

`[-7,\infty)`