Question

Can someone help me the answer choices are still the same for the rest of the questions

Answer 1

Exact perimeters given coordinates are ugly, the sum of a bunch of square roots. A calculator approximation isn't so bad, especially when the choices are so far apart; we can just keep one decimal place.

There's only one rule in play, that the length of a segment with endpoints (a,b) and (c,d) is given by the Pythagorean Theorem as

`l = √((a-c)^2 + (b-d)^2)`

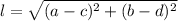
It's going to be too boring for me to do more than one or two, so hopefully you'll learn how and do the rest yourself.

E(2,9),F(2,2),G(10,2)

`EF = √( (2-2)^2 + (9-2)^2) = 7 \quad`

`EG = √((2-10)^2+(9-2)^2)=√(8^2+7^2)=√(113)\approx 10.6`

`FG=√((2-10)^2+(2-2)^2) = 8`

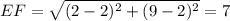
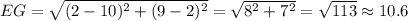
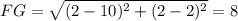
Of course there's a shortcut when one of the coordinates between the endpoints is the same; then we can just skip the square root.

`EF = |9-2|=7`

`DF = |2-10|=8`

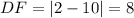
So an approximate perimeter of 7+8+10.6=25.6

First choice

One more, a quadrilateral

M(1,8), N(9,8), O(9,2), P(1,2)

`MN = 9-1 = 8`

`NO = 8 -2 = 6`

`OP=9-1 = 8`

`PM=|2-8|=6`

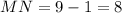
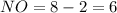
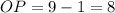
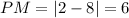
No square roots needed for that one, which is apparently a rectangle, perimeter 8+6+8+6=28

Second choice

I leave the rest for you