Question

Rahim is constructing a proof to show that the opposite angle of a quadrilateral in a circle are supplementary what step would be the first in his proof

Answer 1

The first step in his proof should be the givens if they are provided to you. If they aren't when solving a proof, I like to look for stuff that i know is congruent in the pictures and then using theorems and postulates complete the proof.

Answer 2

First step to prove that opposite angle of a quadrilateral in a circle are supplementary is to find the intercepted arc of opposite angles of cyclic quadrilateral.

Explanation:

Cyclic quadrilateral:

Cyclic quadrilateral is a quadrilateral which lie on a circle.

As shown in figure, ABCD is a cyclic quadrilateral. First step to show that the opposite angle of a quadrilateral ABCD in a circle are supplementary is to find the intercepted arc of opposite ∠A and ∠C of cyclic quadrilateral.

as shown in figure intercepted are of ∠A is Arc(BCD) and intercepted arc of ∠C is Arc(DAB).

Therefore,

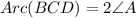`Arc(BCD)=2\angle A`...................(1)

and

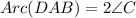`Arc(DAB)=2\angle C`...................(2)

We Know that

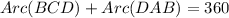`Arc(BCD)+Arc(DAB)=360`..............(3)

Put values of Arc(BCD) and Arc(DAB) in equation (3)

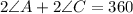`2\angle A+2\angle C=360`.............(4)

`2(\angle A+\angle C)=360`

`\angle A+ \angle C=(360)/(2)`

`\angle A+ \angle C=180`

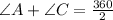
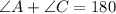
Hence,

opposite angles
`\angle A` and
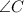`\angle C` of cyclic quadrilateral are supplementary.