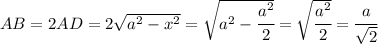Consider the attached image. Let's focus on the triangle ACD. This is a right triangle, and is half of ABC. So, if we maximize the area of ACD, we also maximize the area of ABC.
We know that
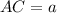 . Let's call the height
. Let's call the height
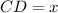 . We can deduce the other leg:
. We can deduce the other leg:
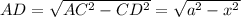
The area of ACD is given by half the product between the base and the height:
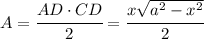
and we want this quantity to be maximized. Again, it is sufficient to maximize the numerator.
To maximize it, let's compute its derivative:
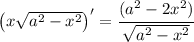
We have a critical point where the derivative equals zero, and a fraction equals zero if and only if its numerator equals zero. So, the critical points are given by
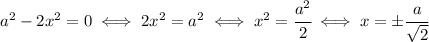
We can't accept a negative solution, so the answer will be
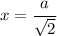
Now, remember that the third side is twice AD, which means