The angle measure of three angle of a triangle are p, q and r.
As, sum of angles of triangle is 180 degrees.
So, p+q+r=180
Angle measure of q is one third of p
q=
 p
p
r is the difference of p and q
r=p-q
As, q=
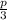
So, r=p-q=p-
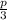
r=

r=
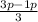
r=
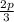
As, p+q+r=180 and q=
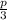 and r=
and r=
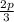
So, we get
p+
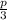 +
+
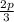 =180
=180
To get rid of fraction, let us multiply the complete equation by 3
3*p+ 3*
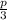 + 3*
+ 3*
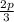 =3*180
=3*180
3p+p+2p=540
6p=540
To solve for p, let us divide by 6 on both sides
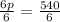
p=90
As, p=90
So, q=
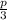
q=
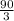
q=30
And, r=
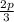
r=
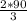
r=

r=60
So, p=90, q=30, r=60
The three angles of triangle are 90,30 and 60