The variable z is directly proportional to x, and inversely proportional to y.

and
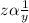
So,
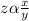
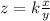
where, k is the constant of proportionality.
When, x=8 and y=18, z is 1.33.
So, plugging x,y and z in z=k\frac{x}{y} to get the value of k we get,
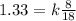
To isolate, k let us multiply by 18 on both sides
1.33*18=k
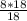
23.99=k
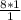
So, 23.99=8k
To solve for k, let us divide by 8 on both sides
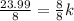
2.99=
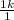
k=3
Let us plug k=3, x=13 and y=22 to solve for z
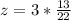
z=
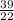
z=1.77
Answer: z=1.77