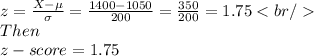Question

Suppose you have a normally distributed set of data pertaining to a standardized test. The mean score is 1050 and the standard deviation is 200. What is the z-score of 1300 point score?

Suppose you have a normally distributed set of data pertaining to a standardized test. The mean score is 1050 and the standard deviation is 200. What is the z-score of 1400 point score?

Answer 1

By the definition of Standard normal probability distribution,

" If X is a normally distributed random variable
`\mu` and
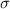`\sigma` are respectively its mean and the standard deviation, then
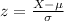`z=(X-\mu)/(\sigma)` is called the standard normal variable. "

Given that, "The normamally distributed set of data pertaining toa standardized test"

(1)

The mean score
`\mu =1050`

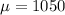
Standard deviation
`= \sigma =200`

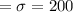
To find the z-score of 1300 point score:

That is,
`X=1300`

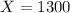
Then the z score is given by

`image`

(2)

The mean score
`\mu =1050`

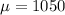
Standard deviation
`= \sigma =200`

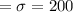
To find the z-score of 1400 point score:

That is,
`X=1400`

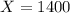
Then the z score is given by

`image`