Question

What is the sum of a 58th arithmetic sequence where the first term is 6 and the last term is 405

Answer 1

Formula to find the sum of nth terms of an arithmetic sequence is:

`S_(n) =(n)/(2) (a_(1) +a_(n))`

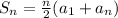
Where,
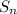`S_(n)` = sum of nth terms.

`a_(1)` = first term.

`a_(n)` = last term.

Now we need to find, sum of a 58th arithmetic sequence where the first term is 6 and the last term is 405 .

So, plug in n = 58,
`a_(1)` = 6 and
`a_(n)` = 405 in the above formula.

`S_(58) =(58)/(2) (6+405)`

=
`(58)/(2) (411)`

=
`(23838)/(2)`

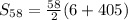
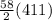
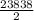
= 11919

So, the sum of 58th terms is 11919.

Hope this helps you!.