Question

Use the given table to determine the appropriate model of the function. x       0             1             2             3             4       f(x)       10             20             40             80             160       linear quadratic cubic exponential

Answer 1

The given table form an exponential function
`y=10(2)^x`.

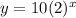Explanation:

Given : Table

x 0 1 2 3 4

f(x) 10 20 40 80 160

To find : Determine the appropriate model of the function?

Solution :

To determine we find the difference of the given function as

• If the first difference is the same value, the model will be linear.

• If the second difference is the same value, the model will be quadratic.

• If the number of times the difference has been taken before finding repeated values, the model may be exponential or some other special equation.

Now, we find the difference

20-10=10

40-20=20

80-40=40

160-80=80

The difference were not equal so the given function is an exponential function as it satisfy the condition of exponential form.

`y=ab^x`

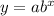
We find a and b by substituting the value of x and y

When, x=0 and y=10

`10=ab^0`

`a=10`

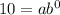
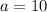
When, x=1 and y=20

`20=ab^1`

`20=10b`

`b=2`

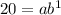
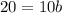
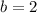
So, The exponential form is
`y=10(2)^x`

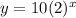
Verification

`y=10(2)^3`

`y=10(8)`

`y=80`

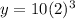
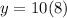
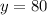
So, at x=3 y is 80.

Therefore, The given table form an exponential function
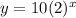`y=10(2)^x`.

Answer 2

Values of x are uniformly spaced, but each value of f(x) is double the one before it. When the function values are a geometric sequence (have a common ratio), the function is exponential.