Question

Can someone please help me with this!?

what would be the area of the shaded region?

A. 17.5
B. 7
C.14
D.35

Answer 1

One way of solving this problem can be Heron's formula. It is a formula that allows us to compute the area of a triangle, knowing the length of its three sides.

For the sake of clarity, let's assume that the point in the top-left lies in the origin, and let's call it point A. Then, the "middle" point is point B, and the bottom-right point is point C.

If we fix the coordinate axis with the origin in A, we have the following coordinates for the three points:

`A = (0,0),\quad B = (4,-1),\quad C = (7,-5)`

We can compute the length of any side using the formula for the distance between two points:

`d(P,Q) = √((P_x-Q_x)^2 + (P_y-Q_y)^2)`

Plugging the approriate values, we get the following lenghts:

`\overline{AB} = √(17),\quad \overline{BC} = 5,\quad \overline{AC} = √(74)`

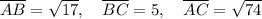
Now that we have the lengths, we can use Heron's formula: given the side lenghts
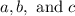`a,b,\text{ and } c` and the semiperimeter
`p`, the area is given by

`A = √(p(p-a)(p-b)(p-c))`

If you plug our values, you will get an area of 6.5. So, unless I'm mistaken, none of the answers seem to mach, whereas 7 seems the best approximation.