Question

Prove segment DE is parallel to segment AB

Answer 1

That's a general triangle in size and shape so this will be a coordinate proof that for any triangle the segment between the midpoint of two sides is parallel to the third side.

Descartes didn't like the cleverness required to do Euclid-like geometry proofs and invented this method (using a coordinate grid) to turn geometry into algebra which is then indeed rather mechanically solved.

Parallel lines have the same slope. The slope of AB is obviously zero, but we calculate it as change in y over change in x, so

`\textrm{slope(AB)} = (B_y - A_y)/(B_x - A_x) = ( 0 - 0)/(x_2 - 0) = 0`

Similarly,

`\textrm{slope(DE)} = (E_y - D_y)/(E_x - D_x) = ( y_1/2 - y_1/2)/( (x_1 + x_2)/2 - x_1/2 ) = 0`

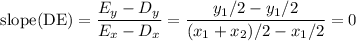
(Both slopes require
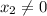`x_2 \\e 0` which is necessary but not sufficient to have a real (non-degenerate) triangle.)

We have equal slopes so parallel line segments and a completed proof.