A geometric series is written as
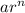 , where
, where
 is the first term of the series and
is the first term of the series and
 is the common ratio.
is the common ratio.
In other words, to compute the next term in the series you have to multiply the previous one by
 .
.
Since we know that the first time is 6 (but we don't know the common ratio), the first terms are
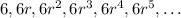 .
.
Let's use the other information, since the last term is
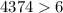 , we know that
, we know that
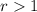 , otherwise the terms would be bigger and bigger.
, otherwise the terms would be bigger and bigger.
The information about the sum tells us that
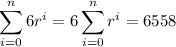
We have a formula to compute the sum of the powers of a certain variable, namely
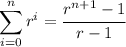
So, the equation becomes
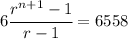
The only integer solution to this expression is
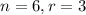 .
.
If you want to check the result, we have

and the last term is
