Question

How to solve this problem?

Answer 1

Very nice handwriting but the math and English are confusing.

Let's assume we're told

`\displaystyle 45 = \sum_(i=1)^9 (x_i - 10)^2`

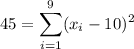
The subscript is important.

I think we're told the similar sum with 11 gives the smallest possible value for the sum. This is a rather cagey way of telling us 11 is the mean of the nine points. The mean is the number which minimizes the sum of squared deviations.

`\displaystyle 45 = \sum_(i=1)^9 (x_i - 10)^2 = \sum x_i^2 - 20 \sum x_i + 9(100)`

`\displaystyle \sum x_i^2= 20 \sum x_i - 900`

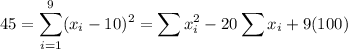
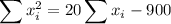
If 11 is the mean, the sum of the points is 9(11)=99.

`\displaystyle \sum x_i^2= 20 (99) - 900 = 1080`

Answer: 1080