Question

Law of sines:

In △BCD, d = 3, b = 5, and m∠D = 25°. What are the possible approximate measures of angle B


only 90°

only 155°

20° and 110°

45° and 135°

Answer 1

the answer is D

Explanation:

Answer 2

In △BCD, d = 3, b = 5, and m∠D = 25°.

According to Sin law,

`(Sin A)/(a) =(Sin B)/(b) =(Sin C)/(c)`

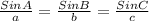
So, When we apply the Sin law to be △BCD

`(Sin B)/(b) =(Sin D)/(d)`

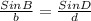
Let us plug in the value of d = 3, b = 5, and m∠D = 25°

`(Sin B)/(5)=(Sin 25 degree)/(3)`

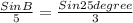
Sin 25 degree according to the calculator is 0.44261

So, Sin 25 degree=0.443

So, we get

\frac{Sin B}{5}=\frac{0.443}{3}

So, To solve for B, let us try to get rid of 5

So, Let us multiply by 5 on both sides.

`5*(Sin B)/(5)=5*(0.443)/(3)`

`(1Sin B)/(1) =(5*0.443)/(3)`

`(1Sin B)/(1) =(2.113)/(3)`

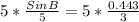
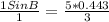
Sin B=0.7043

To solve for B, Let us take inverse of Sin on both

`Sin^(-1) (Sin B)=Sin^(-1)(0.70433)`

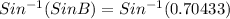
B=Sin^{-1}(0.70433)

B=45 degrees or B= 180 degrees -45 degrees

B=45 degrees or B=135 degrees

As, the Sin B is positive the B lies in first quadrant or second quadrant. As, sin is positive in quadrant 1 or quadrant 2 only. So, to find the angle, B in quadrant 2. we subtract the angle 45 degree from 180 degree.

So, Option D 45° and 135° Answer