Question

Arnulfo deposited $55 into a savings account for which interest is compounded semiannually. according to the rule of 72, what interest rate will cause his money to double in approximately 23 years?

Answer 1

There are 46 interest payments in 23 years so we divide this number into 2*72 = 144.

Required interest rate = 144 / 46 = 3.13 % answer

Answer 2

3.13%

Explanation:

We have been given that Arnulfo deposited $55 into a savings account for which interest is compounded semiannually.

The rule of 72 states that to find the number of years needed to double our money at a given interest rate, we just divide 72 by the interest rate (r).

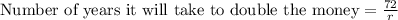`\text{Number of years it will take to double the money}=(72)/(r)`, where r represents the interest rate.

As we have been given that it will take approximately 23 years to double Arnulfo's money, so we can set an equation as:

`23=(72)/(r)`

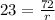
Let us solve for r .

`r=(72)/(23)`

`r=3.1304347826086957\approx 3.13`

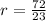
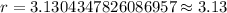
Therefore, at a interest rate of 3.13% Arnulfo's money will be doubled in approximately 23 years.