Question

Dana says any vector can be represented as the sum of two vectors: . ardis says any vector can be represented as the difference of two vectors: . which one, if either, is correct?

Answer 1

Both Dana and Ardis are correct in their respective statements.

This is because a difference of two vectors can always be represented as the sum of a positive vector and a "negative" vector. (Please note that a negative vector is a vector whose direction has been turned
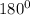`180^0` or has been made "opposite".)

The following explanation will further clarify.

Let us say
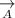`\underset{A}{\rightarrow}` and
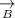`\underset{B}{\rightarrow}` are two vectors. Then the difference of the two vectors can be represented as:

`\underset{R}{\rightarrow} = \underset{A}{\rightarrow}+(-\underset{B}{\rightarrow})` (where
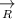`\underset{R}{\rightarrow}` is the resultant vector).

Thus, as we can see a difference of two vectors can be thought of as the sum of two vectors.