Question

PLEASE HELP Consider the three functions below.

f(x) = -6/11(11/2)x g(x) = 6/11 (11/2)-x h(x) = -6/11 (11/2)-x


Which statement is true?


A)The range of h(x) is y > 0.


B)The domain of g(x) is y > 0.


C)The ranges of f(x) and h(x) are different from the range of g(x).


D) The domains of f(x) and g(x) are different from the domain of h(x).

Answer 1

`f(x)=(-6)/(11)*((11)/(2) )^(x)`

Domain : All real numbers since this is an exponential function.

Range : (-∞,0)

`f(x)=(6)/(11)*((11)/(2) )^(-x)`

Domain : All real numbers since this is an exponential function.

Range : (0,∞)

`f(x)=(-6)/(11)*((11)/(2) )^(-x)`

Domain : All real numbers since this is an exponential function.

Range : (-∞,0)

So Option C : )The ranges of f(x) and h(x) are different from the range of g(x).

Answer 2

If these are supposed to be exponential functions

`\displaystyle f(x)=-(6)/(11)\left((11)/(2)\right)^(x)\\\\g(x)=(6)/(11)\left((11)/(2)\right)^(-x)\\\\h(x)=-(6)/(11)\left((11)/(2)\right)^(-x)`

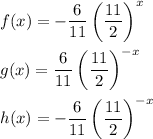
Then they are all defined for all real numbers, so all have the same domain. The range of f and h will be (-∞, 0) and the range of g will be (0, ∞), so these are different.

The appropriate statement choice is ...

... C)The ranges of f(x) and h(x) are different from the range of g(x).