Question

How would I do this problem? In trapezoid PQRS, PQ is parallel to SR. Find the area of PQRS. Leave your answer is simplest radical form.

Answer 1

Suppose that the altitude drawn intersects the base of PQRS at point T

With triangle RTQ, we see that angle T is 90° and angle R is 30°. Since the angles in a triangle always sum to 180°, angle Q is 180° - 90° - 30° = 60°. Thus, triangle RTQ is a 30°-60°-90° right triangle.

The sides of a 30°-60°-90° triangle are in ratio 1:√3:2 (this is in the form (side opposite to 30° angle):(side opposite to 60° angle):(side opposite to 90° angle)). The hypotenuse, the side opposite opposite to the 90° angle, has a length of 24. The altitude of the triangle, the side opposite to the 30° angle, therefore has a length of 24/2 = 12; and the base of the triangle, the side opposite to the 60° angle, has a length of 12√3

Therefore, the area of PQRS is

`=area of left trapezoid +area of triangle`

=
`=(1/2)(6+18)*(12)+(1/2)*(12√(3) *12)`

=
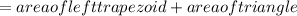
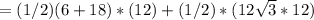
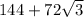`144+72√(3)` units