Question

There is a clown’s face on the top of a spinner. The tip of his hat rotated to (-2, 5) during one spin. What is the cosine value of this function?

A) -2
B) 5
C) 5 sqrt 29/29
D) -2 sqrt 29/29

Answer 1

A lot of the people out there are saying that the answer is negative 2 over sqrt 29. However, I am doing the test, and if you multiply the top and bottom by sqrt of 29, you get D, which is -2 sqrt29/29

Answer 2

The correct option is D.

Explanation:

It is given that the clown’s face on the top of a spinner. The tip of his hat rotated to (-2, 5) during one spin.

In the point (-2,5), x-coordinate is negative and y-coordinate is positive, it means the point lies in 2nd quadrant. In 2nd quadrant cosine values are negative.

From the below figure it is clear that triangle ABO is a right angled triangle, with perpendicular 5 and base 2.

According to the Pythagoras theorem,

`Hypotenuse^2=Perpendicular^2+Base^2`

`Hypotenuse^2=(5)^2+(2)^2`

`Hypotenuse^2=25+4`

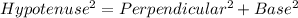
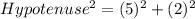
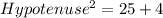
Taking square root both the sides.

`Hypotenuse=√(29)`

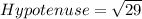
In a right angled triangle,

`\cos \theta=(Base)/(Hypotenuse)`

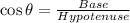
Substitute Base=2 and
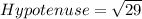`Hypotenuse=√(29)` in the above equation.

`\cos \theta=(2)/(√(29))`

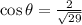
Rationalize the denominator.

`\cos \theta=(2)/(√(29))* (√(29))/(√(29))`

`\cos \theta=(2√(29))/(29)`

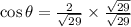
In 2nd quadrant cosine values are negative. So,

`\cos \theta=-(2√(29))/(29)`

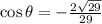
Therefore the correct option is D.