Question

Traveling at an average speed of 50 miles per hour, the trip from point A to point B takes 2 hours. Traveling at an average speed of 40 miles per hour, the same trip takes 2.5 hours.

If time, y, varies inversely with speed, x, how long will the trip take traveling at 45 miles per hour? Round your answer to the nearest hundredth, if necessary.

Answer 1

A

Explanation:

Answer 2

Assuming the traveling speed to be constant, the law that involves space, speed and time is

`s = vt`

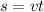
So, the sentence "Traveling at an average speed of 50 miles per hour, the trip from point A to point B takes 2 hours" translates to

`s = 50\cdot 2`

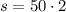
from which we deduce that A and B are 100 miles apart. In fact, we also have

`s = 40\cdot 2.5`

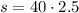
which again yields s = 100.

Now, the question changes the perspective, because it asks for the time needed to travel at a certain speed. Now that we know that the distance is 100 miles, if we travel at 45 miles per hour we have

`100 = 45t`

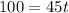
from which we can deduce

`t = \cfrac{100}{45} = 2.\overline{2}`

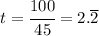
which, rounded to the nearest hundreth, is 2.22.