Denote by
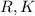 the random variables representing the integer values
the random variables representing the integer values
 , respectively. Then
, respectively. Then
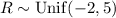 and
and
 , where
, where
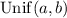 denotes the discrete uniform distribution over the interval
denotes the discrete uniform distribution over the interval
![[a,b]](https://img.qammunity.org/2019/formulas/mathematics/high-school/hycs8sttkhnuq5yfuhyfhr31suzra3n6sc.png) . So
. So
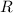 and
and
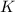 have probability mass functions
have probability mass functions
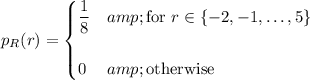
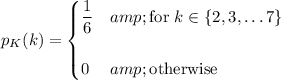
We want to find
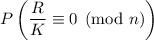 , where
, where
 is any integer.
is any integer.
We have six possible choices for
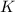 :
:
(i) if
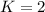 , then
, then
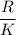 is an integer when
is an integer when
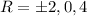 ;
;
(ii) if
 , then
, then
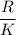 is an integer when
is an integer when
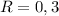 ;
;
(iii) if
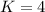 , then
, then
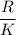 is an integer when
is an integer when
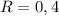 ;
;
(iv) if
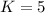 , then
, then
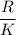 is an integer when
is an integer when
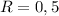 ;
;
(v) if
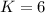 or
or
 , then
, then
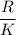 is an integer only when
is an integer only when
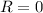 in both cases.
in both cases.
If the selection of
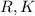 are made independently, then the joint distribution is the product of the marginal distribution, i.e.
are made independently, then the joint distribution is the product of the marginal distribution, i.e.
![p_(R,K)(r,k)=p_R(r)\cdot p_K(k)=\begin{cases}\frac1{48}&\text{for }(r,k)\in[-2,5]*[2,7]\\\\0&\text{otherwise}\end{cases}](https://img.qammunity.org/2019/formulas/mathematics/high-school/wz8nb09yukxc2srps48kb9h45j9x2fqzh2.png)
That is, there are 48 possible events in the sample space. We counted 12 possible outcomes in which
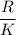 is an integer, so the probability of this happening is
is an integer, so the probability of this happening is
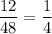 .
.