Answer: 57°
Given : In triangle PQR, the side PQ is 17, QR is 15, and PR is 14.
We use law of cosine formula
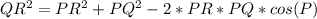
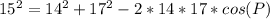
225 = 196 + 289 - 476 cos(P)
225 = 485 - 476 cos (P)
Subtract 485 on both sides
-260 = -476 cos(P)
 = cos(P)
= cos(P)
P =
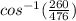
P= 56.89202
So measure of angle P is 57 degrees