Question

Is the relationship shown by the data linear? if so, model the data with an equation. x y 1 –4 7 –7 13 –10 19 –13 the relationship is linear; y + 4 = (x – 1). the relationship is linear; y + 4 = (x – 1). the relationship is not linear. the relationship is linear; y – 1 = (x + 4)?

Answer 1

The given data is:

x 1 7 13 19

y 4 7 10 13

We can check there relationship whether it's linear or not by simply plotting the points on a scatter plot. From the attach scatter plot we can see that the it's linear relationship.

Next step is to find the slope of this data. Formula to find slope is,

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

Let's take the first two points (1,4) and (7,7). So, plug in x1=1, y1=4, x2=7 and y2=7 in the above formula. Hence,

`m=(7-4)/(7-1)`

=
`(3)/(6)`

=
`(1)/(2)`

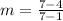
Point slope form of a line is:

`y-y_(1) =m(x-x_(1) )`

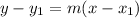
Now we can plug in m=1/2, x1=1 and y1=4 in the above equation. So,

`y-4=(1)/(2) (x-1)`.