Question

Help please! :)

Transform each polar equation in rectangular coordinates and identify its shape.


1. theta= 1.34 radians



2. r=tan(theta)sec(theta)

Answer 1

To solve this question we will make use of the basic relationship between the variables of the polar and cartesian coordinates.

They are:
`tan(\theta)=(y)/(x)`

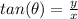
and
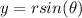`y=rsin(\theta)` and
`x=rcos(\theta)`

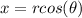
Let us solve the question now:

1.
`\theta=tan^(-1)((y)/(x))= 1.34 radians`

`\therefore (y)/(x)=tan(1.34 radians)`

`(y)/(x)\approx4.26`

`y=4.26x`

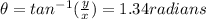
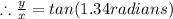
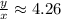
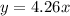
The above is the answer for question 1. It is a straight line which passes through the origin.

2. It is given that:

`r=tan(\theta)sec(\theta)`

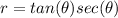
which can be rewritten as:

`r=(sin(\theta))/(cos(\theta)) * (1)/(cos(\theta))`

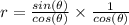
Now, we know that:
`(sin(\theta))/(cos(\theta)) =tan(\theta)=(y)/(x)`

Therefore, we get:

`r=(y)/(x)* (1)/(cos(\theta))`

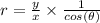
Which gives us, after cross multiplying
`cos(\theta)`:

`rcos(\theta)=(y)/(x)`

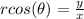
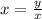`x=(y)/(x)` (Since,
`rcos(\theta)=x`)

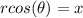Therefore,
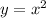`y=x^2` is the final answer we get by cross multiplying x.

This is a parabola.